Math Help for Section 1.1, Page 6

Absolute
Value

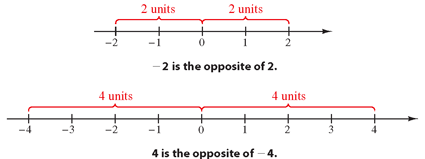
The figures below illustrate the concept of opposites with the real
number line.

Parentheses are useful for denoting the opposite of a negative number.
For example, $ -\left({ -3}\right)$ means the opposite of $-3$ which
is 3. That is,

   
Because opposite numbers lie
the same distance from zero on the real
number line, they have the same absolute value. So, $\left| {5}
\right| = 5$ and $\left| {-5} \right| = 5$ (see figure
below).

You can write this more simply as $\left| {5} \right| =
\left| {-5} \right| = 5.$

   
Another way to define absolute
value is as follows.  If a
is a
real number, then the absolute
value of a
is

    $\left| a \right| = \begin{cases} a
& \text{ if } a\ge 0 \\
-a & \text{ if } a \lt 0
\end{cases}$

   
The definition says that the
absolute value of a nonnegative number is
that number and that the absolute value of a negative number is the
opposite of that number. So, the absolute value of a real number is
either positive or zero (never negative). Note that zero is the only
real number whose absolute value is 0. That is, $\left| {\,0\,} \right|
= 0.$

   
The word expression
means a
collection of numbers and symbols such as $3 + 5$
or $\left| {-4} \right|.$ When asked to evaluate an
expression,
you are to find the number
that is equal to the expression. For instance, $3 + 5 = 8$ and $\left|
{-4} \right| = 4.$

Example
5: Tip

Note in Example 5(d) that $-\left| {-6} \right| =-6$ does not
contradict the fact that the
absolute value of a real number cannot be negative. The expression $ –
\,\left| {-6} \right|$
calls for the opposite of an absolute value (the opposite of a positive
number), so it must be negative.